A simple approximation to a complex mathematical formula to calculate the number of years to double the investment at a given rate of return
The Rule of 72 is a simple and easy way to estimate the approximate time required to double the money for a given annual rate of return and vice versa.
In other words, the Rule of 72 helps an equity investor to know how many years is enough to double the money given the growth rate for his investment.
The mathematical formula is:
I have not used equal to sign (=) but an approximation sign (≈), and we will see why it is an approximation.
Rule of 72 Examples
Now let’s look at a few examples to understand the formula.
If your investment is making a return of 12% per annum, you need 72/12 = 6 years to double the money.
One can also use the rule to find the time it takes for money’s value to halve due to inflation.
If inflation is at 6%, then the purchasing power of the money will become half in 12 years (72 / 6 = 12). In other words, the price of the asset will double in 12 years.
If the inflation decreases from 6% to 4%, an investment will half in 18 years, instead of 12 years.
Understanding The Rule of 72
The Rule of 72 is a simplified approximation of a complex mathematical formula of compound interest for the sake of oral calculation.
Let me share how it is only an approximation.
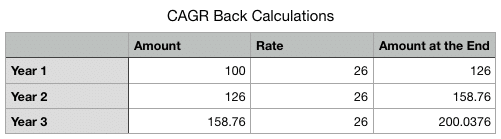
Let’s say you double your money in 3 years. Then, the rate of interest as per the rule of 72 is 24% (72/3).
However, in reality, the rate of interest should be around 26% and not 24%. For example, you can see in the charts below that at a 26% compounding rate of interest, the investment doubles in 3 years and not at 24%.
At 24%, your return won’t be double but only be at 1.9 times. However, it is an approximation of the actual returns.
Here is the chart where ₹100 at the given rate of return will end up after the years:
| Rate of Return | No. of Years | Final Amount |
|---|---|---|
| 2 | 36 | 203.99 |
| 3 | 24 | 203.28 |
| 4 | 18 | 202.58 |
| 6 | 12 | 201.22 |
| 9 | 8 | 199.26 |
| 12 | 6 | 197.38 |
| 15 | 4.8 | 195.59 |
| 18 | 4 | 193.88 |
| 24 | 3 | 190.66 |
| 36 | 2 | 184.96 |
Every number is approximately ₹200. However, as the rule of 72 is an approximation, the rate of return higher than 36 becomes way too vague.
For example, 36% will return to double the money in 2 years, but in reality, you will need to return close to 42%.
Actual Time to Double the Money
So now let’s see the rule of 72 for time – How many years we need to double the money.
| Rate of Return | Rule of 72 | Actual # of Years |
|---|---|---|
| 2 | 36 | 35 |
| 3 | 24 | 23.45 |
| 4 | 18 | 17.68 |
| 6 | 12 | 11.90 |
| 9 | 8 | 8.05 |
| 12 | 6 | 6.12 |
| 15 | 4.8 | 4.96 |
| 18 | 4 | 4.19 |
| 24 | 3 | 3.23 |
| 36 | 2 | 2.26 |
| 50 | 1.4 | 1.71 |
| 72 | 1 | 1.28 |
| 100 | 0.7 | 1 |
As we can see in the above table, the approximation of money to double is better between 4% to 18%. However, it is most accurate between 6% to 12%. As we move higher, the variation to the actual value increases significantly.
The Magic of Doubling the Money
In finance, the magic is in the doubles. If you can double the money ten times in your entire life, you will make 1000x returns. Here is how.
- 1 becomes 2
- 2 becomes 4
- 4 becomes 8
- 8 becomes 16
- 16 becomes 32
- 32 becomes 64
- 64 becomes 128
- 128 becomes 256
- 256 becomes 512
- 512 becomes 1024
It is the same concept that Mr Ramesh Damani explains in this video where you need ten doubles to make 100 Crores from a mere investment of 10 lakhs.
The only thing one needs to understand is how soon you can double each time. For example, if you double every six years, you will need 60 years to reach 100 Crores. But if you double every four years, the time is 40 years.
Final Thoughts
In India, the inflation rate, FD rates or even the return from equity mutual funds over an extended period is 5% to 15%.
So the rule of 72 is a good approximation. Use the rule to find the approximate time when you can double the money.
Finally, I will recommend you start investing early and double the money faster when you are young.




Leave a Reply